Introductie Tot Numerieke Methoden Voor Beginwaardeproblemen
In deze tekst bekijken we enkele numerieke methoden voor het oplossen van beginwaardeproblemen (IVPs) van de vorm
y' = f(x, y)
y(x0) = y0
waar y' de eerste-orde afgeleide is van y naar x.
Werkwijze
De gewone differentiaalvergelijking (ODE) bevat de informatie die nodig is om haar op te lossen. De vergelijking y' = f(x, y) geeft de eerste-orde afgeleide van y als een functie van x en y. Omdat de eerste-orde afgeleide van een functie beschrijft hoe deze functie varieert, is de oplossing van een ODE een verzameling functies die variëren zoals beschreven door de ODE.
Voorbeeld 1
Beschouw de eenvoudige ODE y' = 0. Deze ODE zegt dat haar oplossingen niet veranderen, de oplossingen zijn dus de constante functies y = c, met c een constante.
Voorbeeld 2
De ODE y' = 1/x heeft als oplossingen y = ln(x) + c, met c een constante. Merk op dat alle oplossingen dezelfde afgeleide hebben, omdat y' niet afhangt van y.
De informatie in een ODE kan ook grafisch voorgesteld worden, als een gericht veld. Een gericht veld associeert een richting met elk punt in het vlak. Zo wordt elk punt (x, y) geassocieerd met richting y' of f(x, y). Dit wordt grafisch weergegeven door een lijnstukje met richtingscoëfficiënt y' te tekenen door het punt (x, y). Onderstaande figuur toont een voorbeeld van een gericht veld (uiteraard wordt niet door elk punt een lijnstukje getekend):
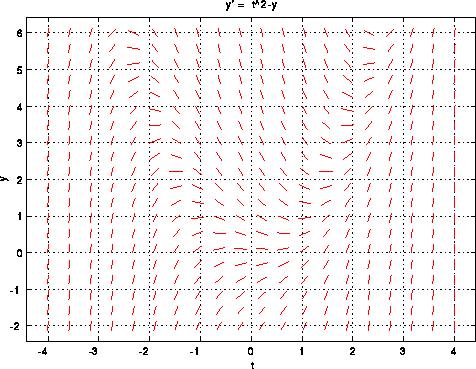Gericht veld
© 1996 - Department Of Mathematics - Oregon State University
Omdat een oplossing van een ODE moet variëren zoals beschreven door de ODE, moet deze oplossing in elk punt (x, y) richting y' hebben, en dus raken aan het lijnstuk dat getekend werd door dit punt. Op deze manier is het mogelijk de oplossingen te schetsen:
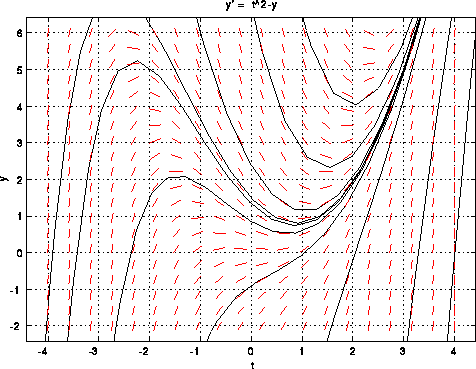Geschetste oplossingen
© 1996 - Department Of Mathematics - Oregon State University
Omdat oplossingen niet kunnen snijden (anders zouden er in het snijpunt twee verschillende richtingen zijn), is het enkel nog nodig om een beginpunt te kiezen. Wanneer een beginpunt gekozen is, zal de ODE vertellen in welke richting de oplossing moet gaan en is het dus mogelijk de oplossing door dit punt te benaderen. Dit is het idee waarop numerieke methoden voor beginwaardeproblemen gebaseerd zijn.
De Methode Van Euler
De methode van Euler is erg eenvoudig. Ze werkt als volgt:
- Kies een beginpunt
(x0, y0). - Bepaal de richting die de oplossing moet hebben in dit punt. Deze richting wordt gegeven door
k = f(x0, y0). - Kies een stapgrootte
hlangs de X-as en volg de rechte met richtingktot een benadering voory(x0 + h)gevonden wordt. - We vinden een nieuw punt
(x1, y1) = (x0 + h, y0 + hk)waar het algoritme opnieuw kan uitgevoerd worden: - Bepaal de richting die de oplossing moet hebben in dit punt. Deze richting wordt gegeven door
k = f(x1, y1). - Volg de rechte met deze richting tot een benadering voor
y(x1 + h)gevonden wordt. - We vinden een nieuw punt
(x2, y2) = (x1 + h, y1 + hk). - ...
Voorbeeld 3
We passen de methode van Euler toe op de ODE y' = 1/x met beginpunt (x0, y0) = (1, 0). De richting die de oplossing moet hebben in dit punt is k = y'(x0) = 1/x0 = 1. Dit wordt weergegeven op onderstaande figuur (de exacte oplossing wordt getekend in blauw, het lijnstuk waaraan de oplossing moet raken in het punt (x0, y0) wordt getekend in magenta):
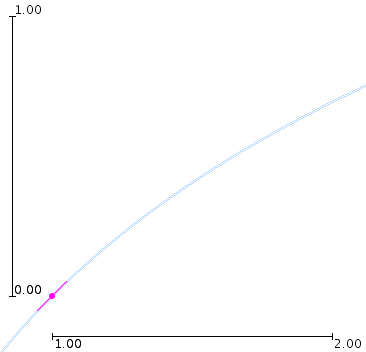Methode van Euler - Bepalen van richting k
Vervolgens kiezen we een stapgrootte h = 1 en volgen we de rechte met richting k tot we een benadering vinden voor y(x0 + h) = y(2). Deze benadering wordt gegeven door y0 + hk = 1. We vinden een nieuw punt (x1, y1) = (x0 + h, y0 + hk) = (2, 1), zoals te zien is op onderstaande figuur (de benaderde oplossing is getekend in rood, de rode stippellijn toont de fout in de benadering van y(2)):
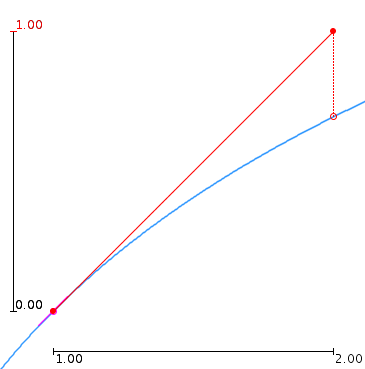Methode van Euler - Benaderde oplossing
Voorbeeld 4
We passen de methode van Euler een aantal keer toe op het IVP met ODE y' = y en beginpunt (0, 1) en vinden een aantal punten. Door deze punten wordt een benadering van de oplossing getekend, zoals in onderstaande figuur (de exacte oplossing wordt in het zwart getekend, de benadering in het rood):
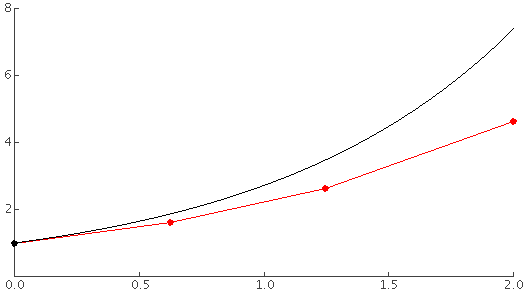Methode van Euler - Meerdere stappen
Een Verbeterde Methode Van Euler
Merk op dat een benaderde oplossing bekomen met de methode van Euler meestal te hoog of te laag ligt, als de oplossing respectievelijk concaaf (Voorbeeld 3) of convex (Voorbeeld 4) is in de buurt van het beginpunt. We kunnen deze informatie dus gebruiken om de methode van Euler te verbeteren door de richting k aan te passen, zoals gebeurt in de gemodificeerde methode van Euler:
- Kies een beginpunt
(x0, y0). - Bepaal de richting die de oplossing moet hebben in dit punt. Deze richting wordt gegeven door
k1 = f(x0, y0). - Kies een stapgrootte
hlangs de X-as en volg de rechte metk1tot een benadering voory(x0 + h)gevonden wordt. - In dit punt berekenen we een nieuwe richting
k2 = f(x0 + h, y0 + hk1). Merk op dat het lijnstukje door dit punt raakt aan een andere oplossing dan de oplossing door(x0, y0), maar de richting van dit lijnstukje is hopelijk niet erg verschillend van de richting van het lijnstukje inx0 + hdat raakt aan de oplossing door(x0, y0). - De uiteindelijke richting wordt
k = (k1 + k2) / 2. Richtingk2wordt dus gebruikt om richtingk1te corrigeren. - We vinden een nieuw punt
(x1, y1) = (x0 + h, y0 + hk)waar het algoritme herhaald kan worden.
Voorbeeld 5
We gebruiken hetzelfde IVP als in Voorbeeld 3: y' = 1/x met beginpunt (x0, y0) = (1, 0). We weten uit Voorbeeld 3 dat k1 = 1 en dat deze richting, gebruikt met stapgrootte h = 1, ons leidt naar het punt (x0 + h, y0 + hk1) = (2, 1). In dit punt berekenen we k2 = f(x0 + h, y0 + hk1) = f(2, 1) = 0.5. Dit is te zien op onderstaande figuur (de grijze lijn is de oplossing door (2, 1)):
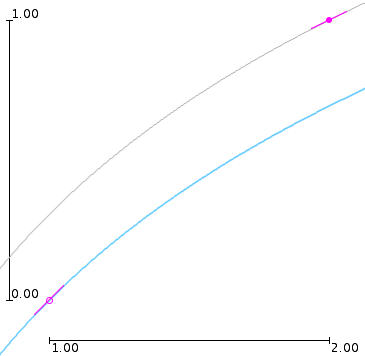Gemodificeerde methode van Euler - Berekenen van richtingen
Het gemiddelde van deze richtingen is k = (k1 + k2) / 2 = 0.75 en we vinden dat (x1, y1) = (x0 + h, y0 + hk) = (2, 0.75), zoals te zien is op onderstaande figuur. Merk op hoe k2, kleiner dan k1, de richting k verlaagd en ook verbeterd.
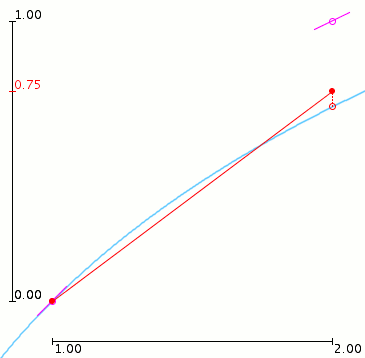Gemodificeerde methode van Euler - Benaderde oplossing
Verdere Verbeteringen
Om betere resultaten te verkrijgen kunnen meer complexe methoden gebruikt worden. Het is uiteraard ook mogelijk om de stapgrootte te verkleinen. Er moet dus steeds een evenwicht gezocht worden tussen de nauwkeurigheid van de resultaten en het vereiste rekenwerk.